Ряды динамики: понятие и классификация. Показатели уровней ряда динамики. Примеры решения задач
Показатели динамики: темп роста и темп прироста

Темп роста (Тр) — это показатель интенсивности изменения уровня ряда, который выражается в процентах, а в долях выражается коэффициент роста (Кр).
Кр определяется как отношение последующего уровня к предыдущему или к показателю принятому за базу сравнения.
Он определяет, во сколько раз увеличился уровень по сравнению с базисным, а в случае уменьшения — какую часть базисного уровня составляет сравниваемый.
Рассчитываем коэффициент роста, умножаем на 100 и получаем темп роста
Коэффициент роста может быть рассчитан по формулам:
Также темп роста может определяться так:
Темп роста всегда положителен. Между цепным и базисным темпами роста существует определенная взаимосвязь: произведение цепных коэффициентов роста равно базисному коэффициенту роста за весь период, а частное от деления последующего базисного темпа роста на предыдущий равно цепному темпу роста.
Абсолютный прирост
Абсолютный прирост характеризует увеличение (уменьшение) уровня ряда за определенный промежуток времени. Он определяется по формуле:
1. Абсолютный прирост (цепной):
2. Абсолютный прирост (базисный):
где уi — уровень сравниваемого периода;
Уi-1 — Уровень предшествующего периода;
У0 — уровень базисного периода.
Цепные и базисные абсолютные приросты связаны между собой таким образом: сумма последовательных цепных абсолютных приростов равна базисному, т. е. общему приросту за весь промежуток времени:
Абсолютный прирост может быть положительным или отрицательным знак. Он показывает, на сколько уровень текущего периода выше (ниже) базисного, и таким образом измеряет абсолютную скорость роста или снижение уровня.
Темп прироста
Темп прироста (Тпр) показывает относительную величину прироста и показывает, на сколько процентов сравниваемый уровень больше или меньше уровня, принятого за базу сравнения.
Он может быть как положительным, так и отрицательным или равным нулю, он выражается в процентах и долях (коэффициенты прироста); рассчитывается как отношение абсолютного прироста к абсолютному уровню, принятому за базу:
Темп прироста можно получить из темпа роста:
Коэффициент прироста может быть получен таким образом:
Абсолютное значение 1%-го прироста
Абсолютное значение 1% прироста (А%) — это отношение абсолютного прироста к темпу прироста, выраженный в процентах и показывает значимость каждого процента прироста за тот же период времени:
Абсолютное значение одного процента прироста равно сотой части предыдущего или базисного уровня. Оно показывает, какое абсолютное значение скрывается за относительным показателем — одним процентом прироста.
Примеры расчетов показателей динамики
Перед изучением теории по теме показатели динамики Вы можете посмотреть примеры задач по нахождению: темпа роста, темпа прироста, абсолютного прироста, средних величин динамики
Пример 1. Расчет среднемесячного темп роста объема продаж
Пример 2. Определение всех показателей динамики (подробный расчет)
Пример 3. Расчет цепных, базисных и средних показателей динамики
О показателях динамики
При исследовании динамики общественных явлений возникает трудность описания интенсивности изменения и расчета средних показателей динамики в контрольных по статистике, которые задают студентам.
Анализ интенсивности изменения во времени происходит с помощью показателей, которые получаются вследствие сравнения уровней. К этим показателям относят: темп роста, абсолютный прирост, абсолютное значение одного процента прироста.
Для обобщающей характеристики динамики исследуемых явлений определяется средний показатели: средние уровни ряда и средние показатели изменения уровней ряда. Показатели анализа динамики могут определяться по постоянной и переменным базам сравнения.
Здесь принято называть сравнимый уровень отчетным, а уровень, с которого производится сравнение, — базисным.
Для расчета показателей динамики на постоянной базе, нужно каждый уровень ряда сравнить с одним и тем же базисным уровнем.
В качестве базисного используют только начальный уровень в ряду динамики или уровень, с которого начинается новый этап развития явления. Показатели, которые при этом рассчитываются, называются базисными.
Для расчета показателей анализа динамики на переменной базе нужно каждый последующий уровень ряда сравнить с предыдущим. Вычисленные показатели анализа динамики будут называться цепными.
Ряды динамики 9

Оглавление
Введение2
1. Понятие и классификация рядов динамики4
1.1 Понятие о статистических рядах динамики4
1.2 Требования, предъявляемые к рядам динамики7
1.3 Тенденция и колеблемость в рядах динамики11
1.4 Структура ряда динамики. Задачи, решаемые с помощью рядов динамики. Взаимосвязанные ряды динамики12
2.Показатели, рассчитываемые на основе рядов динамики14
2.1 Показатели изменения уровней ряда динамики14
2.2 Средние показатели в рядах динамики17
3.Проверка ряда на наличие тренда. Непосредственное выделение тренда21
4.Сезонные колебания и волны24
5.Прогнозирование26
5.1Элементы прогнозирования социально-экономических процессов26
5.2.Метод аналитического выравнивания и прогнозирование28
Заключение30
Список использованных источников31
Практическая часть32
Введение
В современном обществе статистика стала одним из важнейших инструментов управления национальной экономики.
Понятие любого управленческого решения требует предварительного анализа имеющейся ситуации, основывается на просчете вариантов развития, сравнении этих вариантов, оценке точности прогнозов, вероятности ошибок. Методическую базу для решения этих вопросов представляет статистика.
Главной ее задачей является исчисление и анализ статистических показателей, благодаря чему управляющие органы получают всестороннюю характеристику объекта, будь то вся национальная экономика или отдельные ее отрасли, предприятия и их подразделения.
Полная и достоверная статистическая информация является тем необходимым основанием, на котором базируется процесс управления экономикой. Вся информация, имеющая народнохозяйственную значимость, в конечном счете, обрабатывается и анализируется с помощью статистики.
Именно статистические данные позволяют определить объемы валового внутреннего продукта и национального дохода, выявить основные тенденции развития отраслей экономики, оценить уровень инфляции, проанализировать состояние финансовых и товарных рынков, исследовать уровень жизни населения и другие социально-экономические явления и процессы.
Овладение статистической методологией – одно из условий познания конъюнктуры рынка, изучения тенденций и прогнозирования, принятия оптимальных решений на всех уровнях деятельности.
Сложной, трудоемкой и ответственной является заключительная, аналитическая стадия исследования.
На этой стадии рассчитываются средние показатели и показатели распределения, анализируется структура совокупности, исследуется динамика и взаимосвязь между изучаемыми явлениями и процессами. На всех стадиях исследования статистика использует различные методы.
Методы статистики – это особые приемы и способы изучения массовых общественных явлений. Целью данной работы является рассмотрение и изучение рядов динамики, а также решение задач.
1. Понятие и классификация рядов динамики
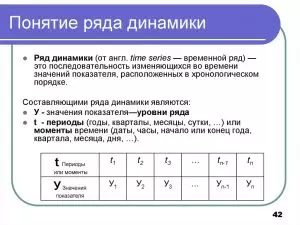
Ряды динамики – ряд численных данных, размещенных в хронологической последовательности. Их также называют динамическими рядами, временными рядами.
Ряд динамики характеризует величину изучаемого явления на конкретный момент или за определенный период времени.
В каждом ряду динамики имеется два основных элемента :
1.показатель времени t;
2.соответствующие им уровни развития изучаемого явления y.
Таблица 1.Число жителей России в 2004-2009 гг. в млн.чел, на 1 января.
В качестве показаний времени в рядах динамики выступают либо определенные даты (моменты), либо отдельные периоды (годы, кварталы, месяцы, сутки).
Уровни рядов динамики отображают количественную оценку (меру) развития во времени изучаемого явления. Они могут выражаться абсолютными, относительными или средними величинами.
Ряды динамики различаются по следующим признакам:
1)По времени. В зависимости от характера изучаемого явления уровни рядов динамики могут относиться или к определенным датам (моментам) времени, или к отдельным периодам. В соответствии с этим ряды динамики подразделяются на моментные и интервальные.
Моментные ряды динамики отображают состояние изучаемых явлений на определенные даты (моменты) времени. Примером моментного ряда динамики является следующая информация о списочной численности работников магазина в 2009 году (таб. 2):
Таблица 2. Списочная численность работников магазина в 2009 году
Особенностью моментного ряда динамики является то, что в его уровни могут входить одни и те же единицы изучаемой совокупности.
Хотя и в моментном ряду есть интервалы – промежутки между соседними в ряду датами, величина того или иного конкретного уровня не зависит от продолжительности периода между двумя датами. Так, основная часть персонала магазина , составляющая списочную численность на 1.01.
2009, продолжающая работать в течение данного года, отображена в уровнях последующих периодов. Поэтому при суммировании уровней моментного ряда может возникнуть повторный счет.
Посредством моментных рядов динамики в торговле изучаются товарные запасы, состояние кадров, количество оборудования и других показателей, отображающих состояние изучаемых явлений на отдельные даты (моменты) времени.
Интервальные ряды динамики отражают итоги развития (функционирования) изучаемых явлений за отдельные периоды (интервалы) времени.
Примером интервального ряда могут служить данные о розничном товарообороте магазина в 2000 – 2004 гг. (таб. 3):
Таблица 3.Объем розничного товарооборота магазина в 1987 – 1991 гг.
Каждый уровень интервального ряда уже представляет собой сумму уровней за более короткие промежутки времени. При этом единица совокупности, входящая в состав одного уровня, не входит в состав других уровней.
Особенностью интервального ряда динамики является то, что каждый его уровень складывается из данных за более короткие интервалы (субпериоды) времени.
Например, суммируя товарооборот за первые три месяца года, получают его объем за I квартал, а суммируя товарооборот за четыре квартала, получают его величину за год, и т. д.
При прочих равных условиях уровень интервального ряда тем больше, чем больше длина интервала, к которому этот уровень относится .
Свойство суммирования уровней за последовательные интервалы времени позволяет получить ряды динамики более укрупненных периодов.
Посредством интервальных рядов динамики в торговле изучают изменения во времени поступления и реализации товаров, суммы издержек обращения и других показателей, отображающих итоги функционирования изучаемого явления за отдельные периоды.
Статистическое отображение изучаемого явления во времени может быть представлено рядами динамики с нарастающими итогами.
Их применение обусловлено потребностями отображения результатов развития изучаемых показателей не только за данный отчетный период, но и с учетом предшествующих периодов. При составлении таких рядов производится последовательное суммирование смежных уровней.
Этим достигается суммарное обобщение результата развития изучаемого показателя с начала отчетного периода (года, месяца , квартала и т. д.).
Ряды динамики с нарастающими итогами строятся при определении общего объема товарооборота в розничной торговле. Так, обобщением товарно–денежных отчетов за последние операционные периоды (пятидневки, недели, декады и т. д.).
2)По форме представления уровней. Могут быть построены также ряды динамики, уровни которых представляют собой относительные и средние величины. Они также могут быть либо моментными, либо интервальными.
В интервальных рядах динамики относительных и средних величин непосредственное суммирование уровней само по себе лишено смысла, так как относительные и средние величины являются производными и исчисляются через деление других величин.
3)По расстоянию между датами или интервалам времени выделяют полные или неполные ряды динамики.
Полные ряды динамики имеют место тогда, когда даты регистрации или окончания периодов следуют друг за другом с равными интервалами. Это равноотстоящие ряды динамики. Неполные – когда принцип равных интервалов не соблюдается.
4)По числу показателей можно выделить изолированные и комплексные (многомерные) ряды динамики. Если ведется анализ во времени одного показателя, имеем изолированный ряд динамики. Комплексный ряд динамики получается в том случае, когда в хронологической последовательности дается система показателей, связанных между собой единством процесса или явления.
1.2 Требования, предъявляемые к рядам динамики
1)Основным условием для получения правильных выводов при анализе рядов динамики является сопоставимость его элементов.
Ряды динамики формируются в результате сводки и группировки материалов статистического наблюдения. Повторяющиеся во времени ( по отчетным периодам) значения одноименных показателей в ходе статистической сводки систематизируются в хронологической последовательности.
Задачи по рядам динамики
Теория по решению задач.
Рядом динамики называется ряд статистических чисел, которые характеризуют изменение величины общественного явление во времени.
Моментный ряд динамики – это ряд динами, уровни которого характеризуют размеры общественно-экономических явлений по состоянию на определенный момент.
В моментных рядах динамики средние уровни вычисляются двумя способами:
1) если ряд динамики имеет равные промежутки времени между двумя составными датами:
, где
– средний уровень ряда динамики;
у – абсолютные уровни ряда динами;
n – число абсолютных уровней ряда динамики.
2) если ряд динамики имеет неодинаковые промежутки времени между двумя составными датами:
, где
t – периоды времени между датами.
Периодический (интервальный) ряд – это ряд динамики, уровни которого характеризуют размеры общественно-экономических явлений за определенные периоды времени (неделя, месяц, полугодие и т. д.).
Средние уровни в периодических рядах исчисляются как простая средняя арифметическая:
Один из важнейших вопросов, возникающих при изучении рядов динамики – это выявление тенденции развития экономического явления в динамике. Для этой цели применяются разнообразные статистические методы, в частности:
– метод укрупнения периодов:
у1=у1+у2+у3
у2=у4+у5+у6
у3=у7+у8+у9 и т. д.
– метод скользящей средней:
и т. д.
– метод аналитического выравнивания:
, где
t – время
n – число членов ряда
у – исходные уровни ряда динамики
а0 и а1 – параметры уравнения, которые необходимо определять.
Основные показатели рядов динамики:
1. Абсолютный прирост (∆у):
а) базисный ∆уб=уn-уо
б) цепной ∆уц=уn-уn-1
∆уб – абсолютный прирост базисный;
∆уц – абсолютный прирост цепной;
уn – уровень сравниваемый;
у0 – уровень периода, принятого за базу сравнение;
уn-1 – уровень, предшествующий сравниваемому периоду.
2. Средний абсолютный прирост ():
n – число показателей в периоде.
3. Абсолютное значение одного процента прироста (А):
∆Т – темп прироста
4. Темп роста (Т):
– базисный
– цепной
5. Темп прироста (∆Т):
– базисный:
– цепной:
6. Средний темп роста ()
у1, у2, уn –коэффициенты цепного темпа роста
n – число коэффициентов
уо и уn – начальный и конечный абсолютные показатели ряда динамики.
7. средний темп прироста (
Задача по товарообороту
Имеется следующая информация о реализации продуктов сельскохозяйственного производства магазинами города:
Среднегодовая реализация, (тыс. грн.):
Таблица № 1
Квартал | 1998г. | 1999г. | 2000г. |
1 | 340 | 515 | 435 |
2 | 280 | 330 | 420 |
3 | 420 | 438 | 380 |
4 | 510 | 240 | 377 |
Для выявления основной тенденции развития товарооборота произведите сглаживание уровней ряда динамики:
1. Методом укрепления периодов по трем кварталам.
2. Методом скользящей средней.
Ход решения задачи:
1. Метод укрупнения периодов:
у1=у1+у2+у3 у1=340+280+420=1040
у2=у4+у5+у6 у2=510+515 +320=1355
у3=у7+у8+у9 у3=438+240+435=1113
у4=у10+у11+у12 у4=420+380+377=1177
Таким образом, укрупненный ряд динамики имеет следующий вид:
1040; 1355; 1113; 1177.
2. Метод скользящей средней:
Т. о. выровненный ряд динамики примет следующий вид:
346,7; 403,3; 481,7; 451,7; 427,7; 336; 371; 365; 411,7; 292,3.
Задача по приростам
Имеется следующая информация о выпуске продукции заводом за 1996-2001 г. г. (тыс. грн.).
Таблица № 2
Годы | 1996г. | 1997г. | 1998г. | 1999г. | 2000г. | 2001г. |
Валовая продукция | 30,2 | 33,4 | 28,6 | 29,4 | 35,8 | 31,7 |
Определите:
1) абсолютные приросты;
2) темп роста и прироста;
3) абсолютное значение 1 % прироста;
4) средний абсолютный прирост;
5) среднегодовой темп роста и прироста.
Ход решения задачи:
1. Абсолютные приросты:
∆уб=уn-уо ∆уц=уn-уn-1
97г.: 33,4-30,2=3,2 33,4-30,2=3,2
98г.: 28,6-30,2=-1,6 28,6-33.ю4=-4,8
99г.: 29,4-30,2=-0,8 29,4-28,6=0,8
00г.: 35,8-30,2=5.6 35,8-29,4=6,4
01г.: 31,7-30,2=1,56 31,7-35,8=-4,1
2. Темпы роста и прироста:
а) темпы роста:
б) темпы прироста:
или вторым способом:
∆Тб=Тб-1 (или 100 %)
∆Тц=Тц-1 (или 100 %)
97г.: 1,106-1=0,106 (10,6%) 1,106-1=0,106 (10,6%)
98г.: 0,947-1=-0,053 (-5,3%) 0,856-1=-0,144 (-14,4%)
99г.: 0,973-1=-0,027 (-2,7%) 1,028-1=0,028 (2,8%)
00г.: 1,185-1=0,185 (18,5%) 1,218-1=0,218 (21,8%)
01г.: 1,05-1=0,05 (5%) 0,885-1=-0,115 (-11,5%)
3. Определяем абсолютное значение 1 % прироста
97г.: 0,01х30,2=0,302
98г.: 0,01х33,4=0,334
99г.: 0,01х28.6=0,286
00г.: 0,01х29,4=0,294
01г.: 0,01х35,8=0,358
4. Определим средний абсолютный прирост:
или вторым способом:
5. Определим среднегодовой темп роста и прироста:
а) среднегодовой темп роста
вторым способом
б) среднегодовой темп прироста:


